ASME B30.20 & BTH-1: Lifting Beam Design
Below-the-hook lifting devices such as spreader bars and lifting beams must be designed in accordance with ASME BTH-1 and are to be manufactured and used in accordance with requirements of ASME B30.20 which specifies requirements for marking, inspection, construction and operation. The design of lifting beams must meet specific calculation requirements per BTH-1 to verify that the design will be safe and effective for its intended below-the-hook lifting application. By using BTH-1 for designing lifting beams, the different failure modes of the beam will be addressed, and appropriate safety factors will be applied to the design, dependent on the intended use or classification of the beam.
Lifting Device Configuration
The first step in developing a lifting device is to determine the lifting configuration, max lift capacity and max spread (width) that is desired. In this article, we will discuss designing a lifting beam according to ASME BTH-1. Therefore, we are looking at a beam that is lifted from the centre and loaded at the ends. This type of lift subjects the beam to flexure (bending) and shear, with bending stress and lateral torsional buckling being the primary modes of failure.

Classification
After establishing the style and capacity required of the lifting beam, the Design Category and Service Class must be confirmed, according to ASME BTH-1. The design category and service class establish the requirements for safety factor for strength and fatigue that will be used in the remainder of the design calculations for the lifting device. The design category and service class are discussed in more detail in the article: Introduction to Below the Hook Design
Structural Design
ASME BTH-1 specifies design calculations for different types of loading of a lifting device including tension, compression, flexure, shear and combined loading of beams. For lifting beams that are subject to flexure, ASME BTH-1 has calculations that define the maximum allowable bending stress based on beam geometry, material properties, and lateral bracing spacing (the distance between braces that resist lateral displacement of the compression flange or twisting of the beam cross-section). Typically lifting beams do not have bracing to resist either of these movements (a single symmetric cantilever beam with no external bracing to stabilize the beam), therefore the lateral bracing spacing is defined as the distance between the outermost lift points of the lifting beam.
Based on the BTH-1 calculations, if the beam length is short enough the beam yield strength limits the lift capacity of the beam, but if the beam length is over the lateral bracing spacing requirement (per calculations in BTH-1), the buckling strength of the structural member defines the allowable lift capacity of the beam, resulting in a reduced maximum allowable bending stress.
Depending on the features of the lifting beam, additional calculations for connections (bolts, pins and welds) are specified to determine suitable sizing and spacing of each.
Calculations for fatigue are also specified in the standard, dependent on the service class of the bar and bar geometry.
Example: Capacity Reduction of Lifting Beam vs Length
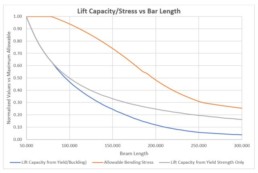
The following chart shows a comparison of a W-Beam lifting beam with lifting capacity based on simple bending stress calculations vs calculations that account for buckling per ASME BTH-1. It shows how there is a reduction in lifting capacity in longer beams due to the instability from lateral torsional buckling.
Allowable bending stress vs beam length per BTH-1 calculations (Orange Plot)
According to BTH-1 calculations, the short beam can be loaded to full yield strength (accounting for safety factors), but as the beam length (or lifting spread) increases, the stress reaches an inflection point where the allowable bending stress starts to drop off. It is at this point where the beam buckling takes over as the limiting factor for load capacity. There are two other inflection points in the curve, one at a beam length of about 180 and another at a beam length of 255. These points are where calculations switch according to BTH-1, due to the beam length (There are several different calculations for allowable stress which are dependent on the beam properties and beam length, with different calculations for different lengths of beams).
Lift capacity vs beam length per BTH-1 calculations (Blue Plot)
The lift capacity of the beam is calculated based on the allowable stress (Orange Plot) and beam length. The calculation includes the weight of the beam.
Lift capacity vs beam length based only on bar yield strength (Gray Plot)
The allowable bending stress is a product of calculations from BTH-1, and the lift capacity is calculated from the allowable bending stress. The bending calculations include bar weight, but do not account for shear stresses. As well, as a comparison, the gray line represents the calculated beam lift capacity based on only bending strength, without accounting for buckling effects.
As can be see from the allowable stress plot, the short beam is permitted to achieve full bending stress (with safety factors), but at a certain point, the allowable bending stress is reduced, to account for the buckling strength of the beam.
Hey, you made it to the end! Congratulations! I hope this article makes you wonder if the engineers you are currently using are just tossing their lifting beam designs into solidworks and applying loads rather than doing the full calculations required by the code. If you are ready to skip the stress of designing your own lifting equipment take a second to check out our store: Basepoing Engineering Store Where you can find fully engineered stamped and certified drawings based on years of experience designing and building spreader bars.
Success! Now check your email to confirm your subscription.
